Chapter 3 - Variables and Assignment Statements¶
The assignment operator¶
In Chapter 1 we saw that one of the key ingredients of problem-solving is being able to store a value using a variable and look it up again later. In Python, you can create a variable just by thinking of a name for it and assigning it a value. Assignment is done with the equals sign “=”, except in Python we don’t call it the equals sign, we call it the assignment operator. For example, we can write:
The first line, x = 42 + 5, is read as “x gets the value 42 + 5”. It is an example of an assignment statement. You can see that after it executes, x has the value 47. Notice when we read an assignment statement, we are careful not to say “is equal to”. An assignment statement doesn’t check whether the two sides are equal, it changes the value of whatever variable on the left. This takes some getting used to!
A good way to think about assignment is that it is really a two-step process:
- Step 1: evaluate the expression on the right-hand side
- Step 2: take its value, and store it in the variable on the left-hand side
It only works right-to-left, so there has to be a variable on the left!
As an example, let’s try writing an assignment statement backwards. Try running the code below, and see what error you get.
Here are some more examples of assignment statements.
Notice that a variable doesn’t have to be a single letter (although there are some restrictions that we will explore shortly).
We sometimes draw a “picture” of the effects of an assignment by putting the value of the variable in a box with a label. A picture like this is called a “memory map,” because in reality the value of each variable is stored in the computer’s memory. After the three assignments above, the memory map would look like this:
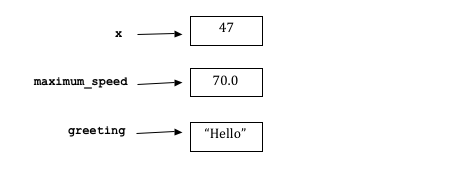
While it is important to be able to sketch a memory map by hand when you are trying to understand a piece of code, we can also use the CodeLens tool. Click on “Show CodeLens” in the example above and step through the code using the “Forward” button.
With that in mind, let’s look at an example to test our understanding of the two-step process used for an assignment statement. Suppose we write:
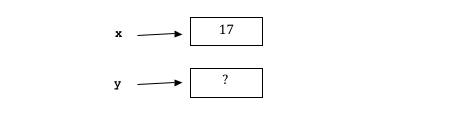
Now, after those three statements execute, what is the value of y? Let’s draw a memory map and follow what’s going on. After the assignment x = 17 we have the following (we’ll put a question mark in y’s box to indicate that it hasn’t been defined yet):
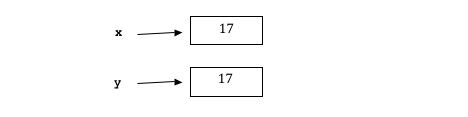
The assignment y = x follows the two-step process. First we evaluate the expression on the right, namely x, which has value 17. Then we take that value, and store it in the variable y. The resulting memory map looks like this:
The next assignment x = 137 stores the value 137 in x, so y still has the value 17.
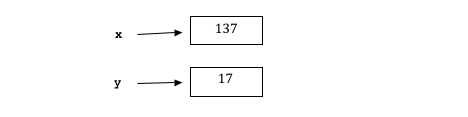
The moral of the story is that the assignment statement x = y really doesn’t mean “x is equal to y”.
Here is another example that looks odd at first, but comes up all the time in programming.
Wait a minute. Does that even make any sense? Well, if this ws a math book, you’d probably ask for your money back, since whatever “x” is, it’s impossible for it to be equal to x + 5. But remember, in Python, the symbol “=” is not an equals sign, it’s the assignment operator. Let’s trace what happens and see if we can figure out what’s going on.
The type of a variable¶
Like any value, a variable has a type. In Python, the type of a variable is determined by the type of the value it stores, and if we later store a different value, the type of the variable can change. (This is a bit weird if you’ve ever seen a language such as Java or C, in which the type of a variable has to be explicitly defined and can never change.)
If you try to use a variable that has never been defined, you’ll get an error. Try this:
We mentioned before that variables don’t have to be single letters, but there are some restrictions. A variable has to be a valid Python identifier, which means that it - must start with a letter or underscore (not a number), - must contain only letters, numbers, or underscores (no other spaces or punctuation), and - can’t be a Python keyword.
There are some conventions too. These are things that the interpreter won’t care about, but that Python programmers find useful.
- Use lowercase letters only
- Use meaningful names for variables that have a particular meaning.
- If there are multiple words, separate them with the underscore character, as in
maximum_speed.
Example¶
Let’s do a problem that uses variables in a simple calculation. Here is the problem we’ll solve: suppose you are given an amount of money in cents, print out how you would make change using quarters, dimes, nickels, and pennies. This is a problem that we have no trouble solving in real life. We just have to analyze how we’re doing it.
Let’s start with a concrete example: Suppose you have to make 67 cents in change. Well, we would probably start by counting out two quarters. Why not three quarters? Well, that would be too much, since 25 goes into 67 only two times.
Are we done? Not quite, since there’s 17 cents left. So you count out the dimes. You only need one dime, since 10 only goes into 17 once.
Now let’s look at what we did a bit more carefully. How did we know how many quarters to use? Well, 25 only goes into 67 two times. In other words, in our minds, we are performing an integer division of 67 by 25:
Two quarters = 67 // 25
How did we know there was 17 cents left? Well, that’s the remainder after we divide 67 by 25. Remember we can get the remainder using the “mod” operator. Here 67 mod 25 is 17:
17 cents left = 67 % 25
Now when we look at the remaining 17 cents, how do we know there will be one dime? Again, 10 goes into 17 just once:
One dime = 17 // 10
And we can get the amount left, 7 cents, by looking at the remainder.
7 cents left = 17 % 10
The same thing works again for finding the number of nickels, and the amount left over is the number of pennies:
One nickel = 7 // 5
Two pennies = 7 % 5
Now, we don’t really care about 67 cents. We want to make change for any amount. Let’s suppose that we have a variable, called amount, that has the initial number of cents for which we need to make change.
The thing is, now that we have worked out a specific example, we know everything we need to know about how to do this problem. Instead of asking how many quarters there are in 67 cents, we ask how many quarters there are in amount cents. To answer this question, we only need to look at how we did it in our specific example. Instead of 67 divided by 25, we write amount divided by 25. We can store the result in a variable to print out later. We might as well call the variable quarters:
quarters = amount // 25
The important thing to notice is that the strategy is exactly the same as it was when making change for 67 cents: we’re just using a variable instead of using the specific value 67.
Next, how did we figure out the amount that was left after counting out the quarters? We took 67 mod 25. So now, we take amount mod 25. We could define a new variable to store the left over amount, but we might as well just update the amount variable, since we will have to do this again each time we get the amount left over.
amount = amount % 25
For the next step, we asked how many dimes were in 17 cents. Where did 17 cents come from? That was the amount left after counting out the quarters.
So now we ask, how many dimes are in amount cents, where
amount now represents the amount left after counting out the quarters.
Again, we only need to mimic what we did in the specific example.
The number of dimes is amount divided by 10, and
The amount left is amount mod 10.
dimes = amount // 10
amount = amount % 10
We do the same thing for the nickels, and the final amount left over is the number of pennies.
nickels = amount // 5
amount = amount % 5
The only thing we need to do in order to finish writing the script is to print out the numbers of quarters, dimes, nickels, and pennies.
Try stepping through the example using CodeLens and look at the effect of each statement.
Before we finish with this example, stop for a moment and look at what we did.
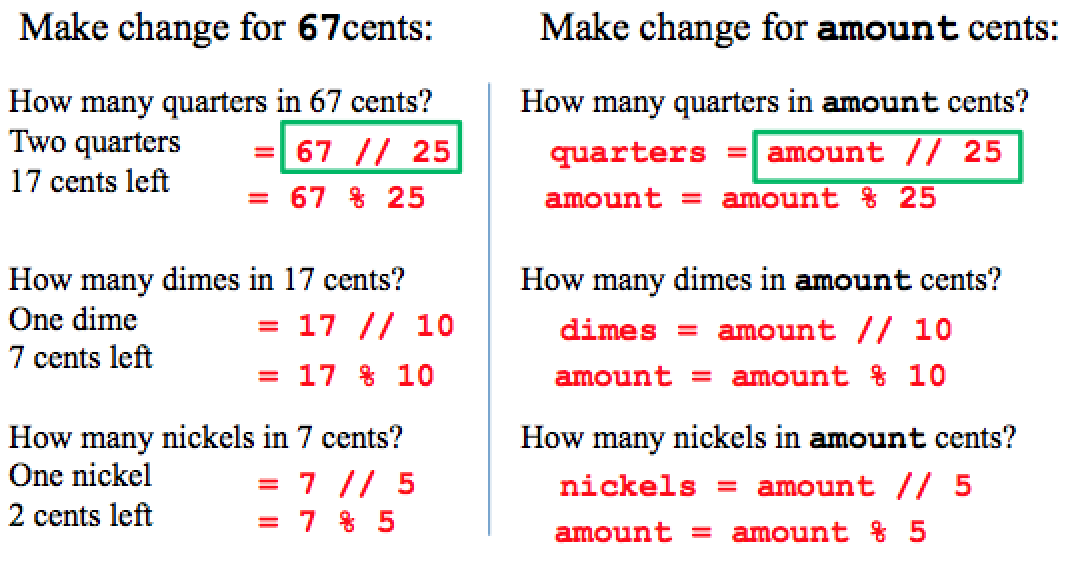
If you compare the left side and the right side of the illustration, the thing to notice is that the general solution to this problem, that works for any amount of change, looks exactly the same as the specific example on the left that gives the answer for 67 cents. That specific example was easy for us to figure out, and doing that first gave us a lot of insight and confidence when we went to write the code. Somewhat ironically, you will find that this is one of the most effective things you can do when you go to start solving a new problem using a computer: get out a pencil and paper, and write out a specific example first!